
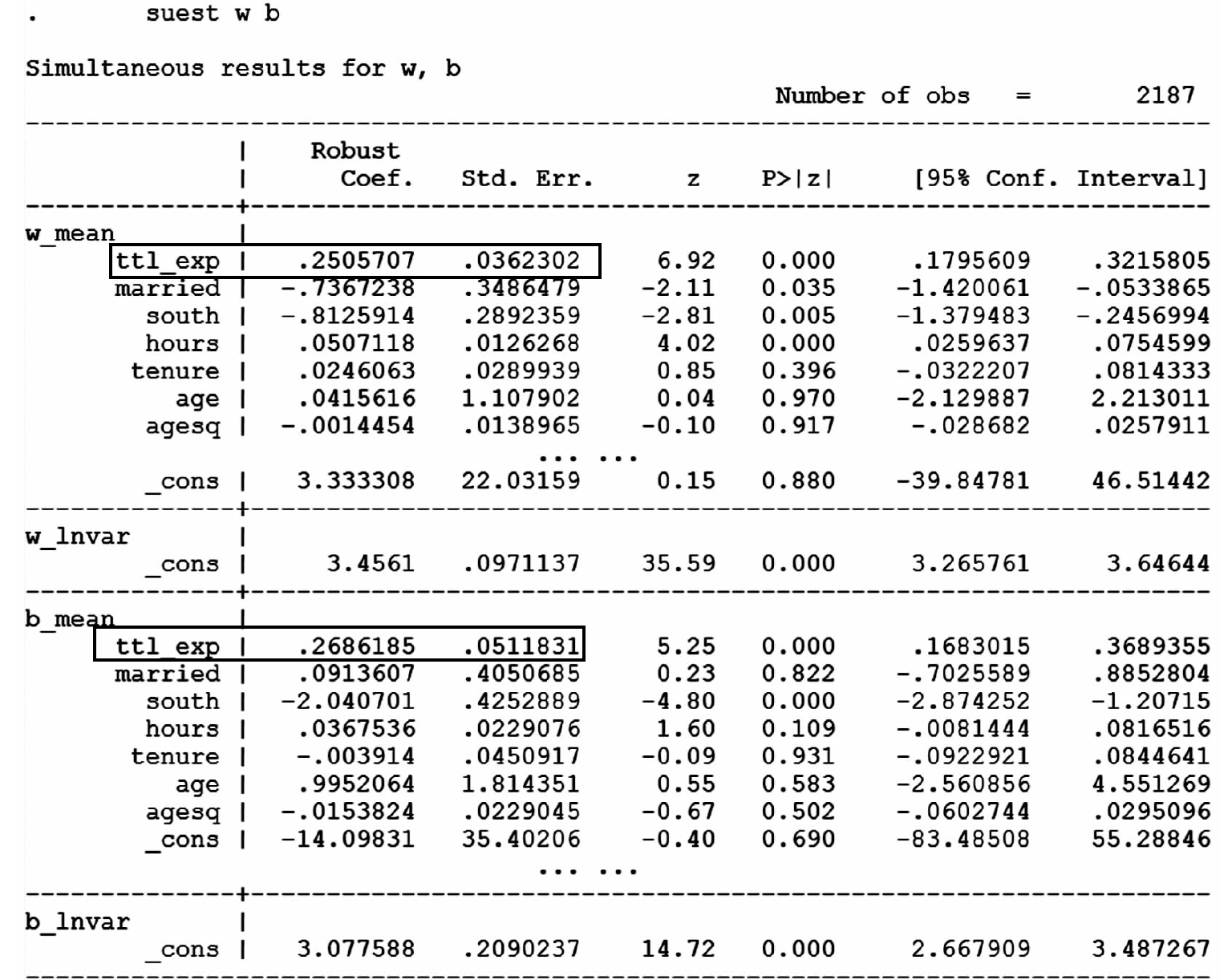
Pooling the models together both lets us test that assertion, as well as get a better estimate of the overall treatment effect. We might then estimate two separate equations: E = B0v + B1v*(Treatment)Į = B0p + B1p*(Treatment)īy saying that I think by default we should think about pooling is basically saying that B1v is going to be close to equal to B1p in the two equations. So say we have a situation with two outcomes, violent crimes and property crimes, and we have one independent variable we are interested in, say whether an individual was subjected to a particular treatment. I think that is the better default for the majority of situations. Most of the time students default to estimating separate equations for each of these outcomes, but in most circumstances I was telling the students they should pool these outcomes into one model.
different crime outcomes for spatial research, different measures of perceptions towards police, different measures of fear of crime, etc.). The most common one is examining different types of delinquency for juveniles (often via surveys), but it comes up in quite a few other designs as well (e.g. Something that came up for many of my students this last semester in my Seminar in Research class is that many were interested in multiple outcomes.


 0 kommentar(er)
0 kommentar(er)
